Sagherian Ladders
April 11, 2020
An unprepared teacher lacks both the problem sequences and articulation to make mathematical topics clear. As a result, lessons commonly begin with questions and/or examples that intimidate a quarter or more of a class’ students. This, combined with verbose explanations, bores and confuses children. It’s common for elementary math teachers to speak for over a minute before asking, requiring, or prompting their students to do anything. By this point, so many students have become disengaged, that the teacher spends the rest of the instructional period managing disciplinary problems and searching for ways to reexplain topics.
While observing elementary math instruction in Chicago Public Schools, Dr. Yoram Sagher, a professor of mathematics at Florida Atlantic University, recognized this reality. He estimated that whenever a teacher talked longer than 15 seconds, most students stopped paying attention. Those who began lessons with questions instead of explanations, encountered a different problem. Ten out of 30 students would raise their hand and the instructor would call on one of them. Feeling rejected, many who weren’t selected became frustrated and angry, leading to disciplinary problems. This dysfunctional dynamic was compounded by a high percentage of students functioning several years behind grade level.
To address these challenges, Dr. Sagher developed a unique method of precision teaching that stimulates focus and engagement, while incorporating reviews into standard instruction. This delivery method involves teachers leading students to understand new topics through a laddered series of questions, using as few words as possible. Instead of calling on individuals, the teacher signals for whole-class responses, which helps them gauge collective class comprehension.
Laddered Instruction
Accumulating mathematical knowledge is like building a tower. Learning any new concept is based on previously established foundations, e.g.
A piece of folded paper illuminates the concept of an angle.
Folding a piece of paper twice, the second time along its crease, creates perpendicular folds and a right angle.
Knowing that a right-angle measures 90 degrees helps children reason that there are 180 degrees in a straight line.
Piecing together any triangle’s vertexes creates straight lines and the realization that there are 180 degrees in any triangle.
Finding missing angles in a triangle leads to the understanding that the exterior angle of a triangle is equal to the sum of its interior opposite angles.
When teachers begin math instruction using grade level questions, there is a conscious or – more likely – subconscious assumption that each of their students have mastered all curricular content leading up to the lesson. This is hardly ever a reality but in the rare cases that it is, students still benefit from laddered, foundational instruction. Beginning with grade level questions can be overwhelming for any child when problems quickly jump in complexity. Answering a series of simple questions before encountering a challenging one develops student confidence and hones their concentration. Concise topical reviews also help children understand the subject’s interconnectivity, which produces greater base knowledge and, in turn, deeper mathematical understanding.
Teachers who ascribe to Dr. Sagher’s laddered instructional approach believe that children have innate mathematical understanding. To learn new concepts, their students simply need an instructor to clear a path that leads them to comprehension. The teacher, therefore, aims to extract the math from their students rather than inserting it through explanations. They begin lessons with simple questions that every student can comfortably answer. Then, gradually, they begin asking more challenging questions until eventually arriving at grade level content (see script below).
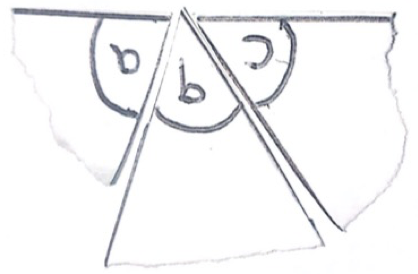
T: (Projects acute angle.) Name the angle.
S: Angle ABC.
T: Is it right, acute, or obtuse?
S: Acute.
T: (Projects:)
T: And this one?
S: Obtuse.
T: (Projects:)
T: This one?
S: Right.
T: How many degrees are in a right angle?
S: 90 degrees.
T: (Writes 90 degrees inside right angle. Points at the other side of the right angle.)
T: How many degrees are in this angle?
S: 90 degrees.
T: (Writes 90 degrees inside the other right angle.)
T: How many degrees are in a straight line?
S: 180 degrees.
T: (Distributes different-size triangles to each student.) Show me your shape.
S: (Hold up triangle.)
T: Name the shape.
S: Triangle.
T: Tear off each angle of your triangle and fit the vertexes together at a point.
S: (Do so.)
T: What do the vertexes form?
S: A straight line.
T: How many degrees are in a triangle?
S: 180 degrees.
Continually immersed in this type of laddered instruction, students learn that their teacher will always keep them in a comfortable learning zone. In turn, they arrive to class confident that they’ll succeed and eager to show off what they know. This heightens children’s concentration and, because they’re not carrying a math complex, leads them to surpass learning they otherwise might never have approached.
Brevity
Over-talking is the measles of the underprepared. People often crutch on verbosity in awkward and/or stressful situations. In these instances, silence has a pulsating effect that increases their anxiety, and rambling becomes a mechanism to cope with the discomfort. When teachers don’t understand the content they’re teaching and/or don’t know how to make it clear to their students, they often babble through their lessons and their words sound like gibberish to whoever is trying to comprehend them. It’s common for these teachers to say 80 or more words before any child in the classroom speaks.
Teachers who practice hyper-brevity say everything that needs to be said but nothing more. Every unneeded word is like a vapor puff in the classroom. The more they’re spoken; the more students need to strain and clear away figurative fog to access the mathematics they’re trying to learn. Precision teaching masters speak less than five words for every one word that their students say. (In the preceding script, the teacher/student word ratio is less than 4:1.)
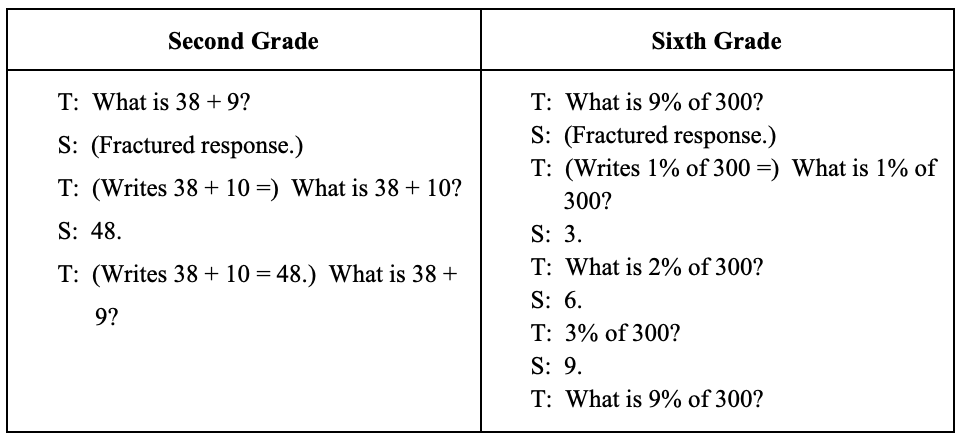
Table 1
When the teacher hears or sees an incorrect answer, they never digress into lengthy explanations as to why certain answers are wrong.
Instead, they concisely offer the correct answer and provide an analogous question to see if students are able to self-correct (see Table 1).
If 90% of the class gets the follow-up question correct, then they move to a greater complexity. If not, they either provide another analogous problem or ask a simpler question. (1)
Table 2
Choral Responses
Cooperating in communal endeavors is integral to being human. Children feel comfort and joy when participating with their classmates. Rather than calling on individuals, teachers signal for choral responses.
While this is not a full proof way of knowing whether or not all students understand, it’s fairly simple for teachers to recognize if 90% of the class answers correctly. (2) Each fractured choral response means that the teacher has asked a question that is collectively too challenging. They then ask a simpler question(s), inserting rungs in their instructional ladder that build back to the complexity that faltered students (see Table 2).
The teacher paces choral responses by training their students to not respond until they hear a sharp, definitive signal, e.g. snapping or clicking a marker on the board. Deeply attuned to their students’ mathematical levels, they plan intricate question sequences with great acuity. By avoiding big jumps in complexity, they’re able to keep unconfident students from feeling discouraged.
This form of precision teaching creates a contagious instructional rhythm, curbs ADHD, and helps all children experience consistent success. (3) Feeling like they are part of the group, struggling students feel less stigmatized when they answer and are more willing to take risks. The efficient instructional pace keeps strong students engaged when questions are simple.
Precision Teaching Scripts:
___
(1) Precision teachers don’t always designate 90% as a mastery benchmark. They might adjust it higher or lower depending on their expectations. Regardless of the percentage they choose, they always aim to ladder their instruction so that 100% of their students are correctly answering several questions/minute.
(2) There is an exception to this rule. Some teachers practice Dr. Sagher’s form of precision teaching using whiteboard exchanges instead of choral responses. This method involves students writing instead of saying answers. What is lost in efficiency and rhythm is made up for in accuracy. Students can mime responses when prompted for a choral response, but cannot do so through whiteboard exchanges.
(3) A master precision teacher, paired with a class that is well-conditioned to work, can create false illusions of instructional speed. Children who are alert and focused respond with alacrity to instructors who carefully sequence questions and don’t over-talk. By tightening transitions and eliminating unnecessary words, lulls are non-existent, a fluid pace emerges, and a mirage of speed is formed. Teachers work with urgency and students comprehend quickly, but the former doesn’t hurry and the latter never feels rushed.